结合代码理解各种注意力机制(一):自注意力机制
transformer中最重要的就是注意力机制,从经典论文Attention is all you need出发,到后来的各种注意力机制的改进。本系列将手撕各种注意力机制,包括但不限于:
- self-attention(SA) 自注意力机制
- multi-head attention(MHA) 多头注意力机制
- multi-query attention(MQA) 分组注意力机制
在此系列的第一篇中,我们聚焦于经典的自注意力机制,mask的注意力机制,以及多头注意力机制的改进。
前置词典和词向量的构建
1. 词典dictionary构建
假设我们有一个句子:
1 | |
然后对句子进行分词,构建词典。
1 | |
打印结果如下:
1 | |
将原来的英文句子转换成对应词典中的索引
1 | |
得到的text_id结果如下:
tensor([0, 7, 1, 3, 4, 6, 8, 5, 2])
2. 词嵌入构建
利用torch.nn.Embedding构建词嵌入,在这里设置的词向量维度为5,方便演示。而实际中,大模型的词向量往往很高,比如在Gpt系列中词向量维度就是12800。
1 | |
得到结果:
1 | |
绘制了一张表格来表示各个词对应的词向量:
自注意力机制实现
流程说明
我们需要将每个词的embedding投影到三个空间中,分别表示query, key, value。
那么投影后的query, key, value向量维度dq, dk, dv是多少呢?需要注意的是,query和key的维度需要相同,而dv可以和dq, dk不同
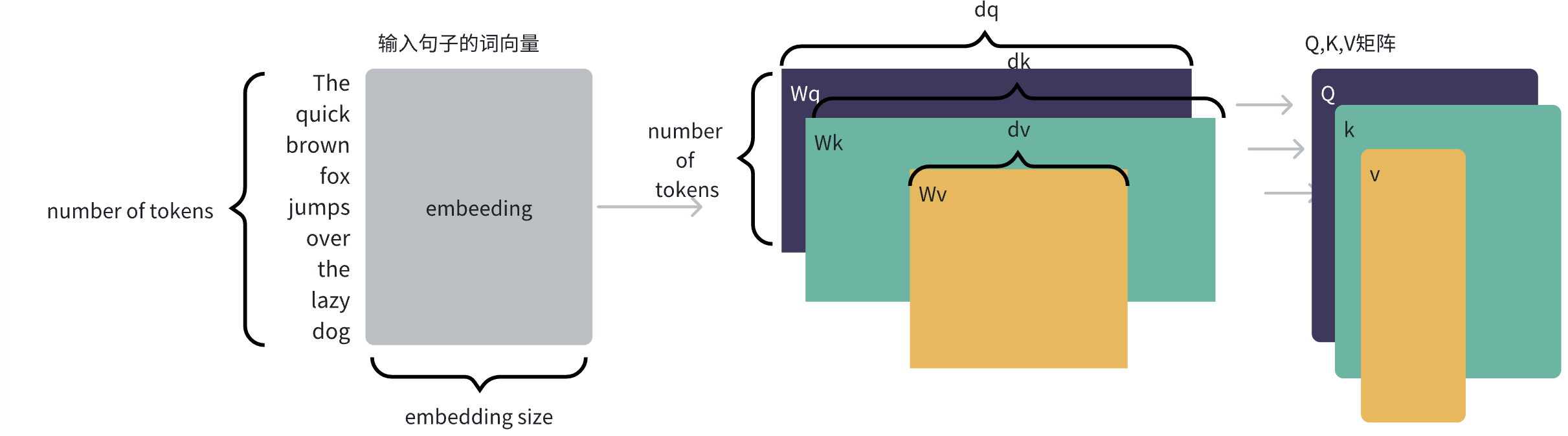
注意力机制计算的公式如下: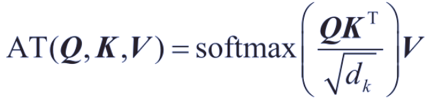
可以根据这个计算流程图来计算: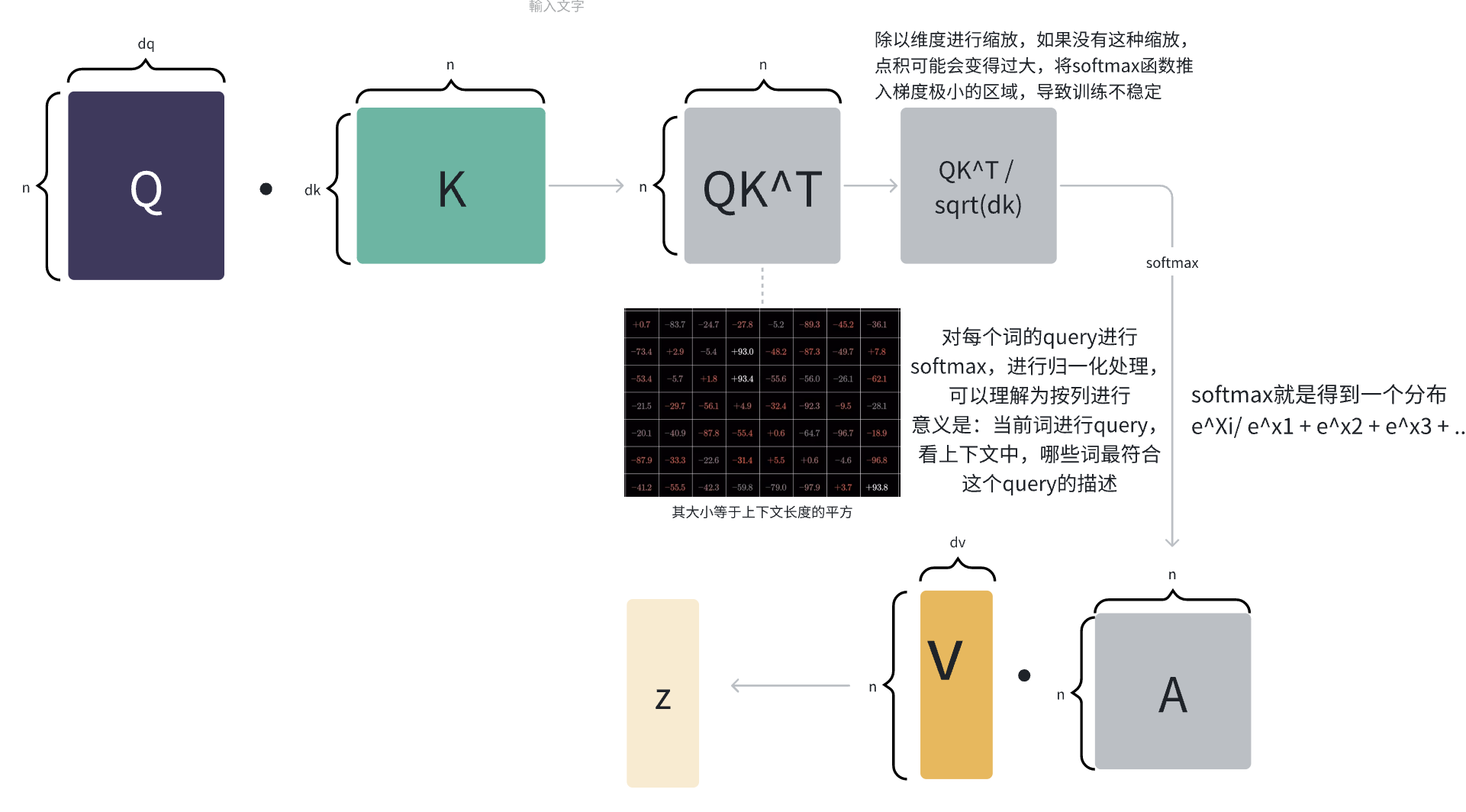
举例类别:
我们新撰写了一篇博客,想要预测博客的阅读量。我们还有一个数据库,里面存放着各种{博客:阅读量}的数据,假设为{1:100, 2:200, 3:300}。
待预测的博客就是query, 数据库里已经有的文章就是key,我们计算待预测的博客和数据库里已经有的文章的相似度,也就是Q @ K.T
假设相似度为{8,4,1}。在这里我们可以注意到,Q @ K.T的形状已经无视了什么embedding size, dim_q, dim_v,而是最简单,最淳朴的{1, 上下文token数},表示的是当前token对上下文的注意力权重。
然后进行softmax操作,将得分进行归一化,得到{0.8,0.15,0.05}。也就是 softmax(Q @ K.T)。我们注意到softmax不会缩维,原来的相似度为{8,4,1},经过归一化后得到的仍然是1*3形状的矩阵。
而阅读量作为value:{100,200,300},我们将相似度与value进行加权求和,即0.8 * 100 + 0.15 * 200 + 0.05 * 300 = 125,就是我们待预测文章的阅读量。
细心的读者可以发现,计算过程中,softmax(Q @ K.T)中 Q @ K.T 还除以了根号dk,这是为什么呢?
因为括号内的值是softmax的输入,而
代码实现
代码是经过结构化的,封装了一个self-attention的类,代码如下:
1 | |
使用这个模块的步骤如下:
1 | |
得到的结果如下,具体的数值就略过,我们查看形状即可:
1 | |
额外添加:因果自注意力机制
在transformer的decoder中,当前token只能关注到之前已经生成的token,而不能看到未来的token,因此,在计算注意力分数时,需要mask掉未来的信息。即注意力分数矩阵长这样:

在代码中实现这个机制也很简单,需要用到2个函数:
- torch.tril()函数,这个函数可以生成一个下三角矩阵,其中对角线以上的元素为1,对角线以下的元素为0。参数diagonal表示刚刚好位于对角线上的元素的值
- torch.masked_fill()函数,这个函数可以对矩阵中的元素进行填充,参数mask.bool()表示将mask矩阵中的元素为True的元素填充为-inf,False的元素保持不变。
实现代码如下:
1 | |
mask矩阵为:
1 | |
attn_score为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
tensor([[-0.0394, -inf, -inf, -inf, -inf, -inf, -inf, -inf,
-inf],
[-0.9510, -1.6893, -inf, -inf, -inf, -inf, -inf, -inf,
-inf],
[-2.9732, -3.2457, -0.2289, -inf, -inf, -inf, -inf, -inf,
-inf],
[-0.5146, -1.5604, 0.4291, 0.2427, -inf, -inf, -inf, -inf,
-inf],
[ 1.9082, -0.0317, 3.1926, 0.7505, 2.3168, -inf, -inf, -inf,
-inf],
[-1.7217, -2.1771, -0.6873, -0.7923, 1.2813, -1.1493, -inf, -inf,
-inf],
[ 0.2187, -0.9201, 0.7226, 0.0409, 1.5223, 0.2587, 0.7383, -inf,
-inf],
[ 1.9516, 0.2456, 2.3482, 1.5573, 1.8757, 1.1425, 0.8713, 1.6937,
-inf],
[-0.8420, -1.8965, -0.7995, -0.2597, 1.3088, -1.2735, -0.3359, 0.2703,
-1.4732]], grad_fn=<MaskedFillBackward0>)
完整的带mask的注意力机制代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import torch
import torch.nn as nn
class MaskSelfAttention(nn.Module):
def __init__(self, d_emb, d_k, d_q, d_v):
torch.manual_seed(0)
super().__init__()
self.d_k = d_k # 方便后面除以维度进行缩放
self.get_query = nn.Linear(d_emb, d_q)
self.get_key = nn.Linear(d_emb, d_k)
self.get_value = nn.Linear(d_emb, d_v)
def forward(self, embed):
query = self.get_query(embed)
key = self.get_key(embed)
value = self.get_value(embed)
attn_score = query @ key.T
mask = torch.triu(torch.ones(attn_score.shape[0],attn_score.shape[0]),diagonal=1)
attn_score = attn_score.masked_fill(mask.bool(),float('-inf'))
attn_score = torch.softmax(attn_score / self.d_k ** 0.5, dim = -1) # 最后一个维度,表示按列进行softmax
attn_score = attn_score @ value
return attn_score
1 | |
1 | |
备注
但实际上,n = 9, d_emb = 5, embedding的形状为[9, 5]
而attn_score的形状为[9, 16]。
我们期望的是经过注意力机制之后,能生成一个和embedding形状相同的向量,称为△E,这样可以和原来的embedding相加,得到新的embedding: E = E + ΔE。 这也是add & normalize 中的add部分。
但目前attn_score的形状和embedding的形状不一致,怎么办呀?所以需要进行调整。
后面在实现的时候,通常还会有一个down_project层,维度为[d_k, d_emb],将attn_score的形状调整到和embedding的形状一致。
理想状况下的self-attention的维度变化如下: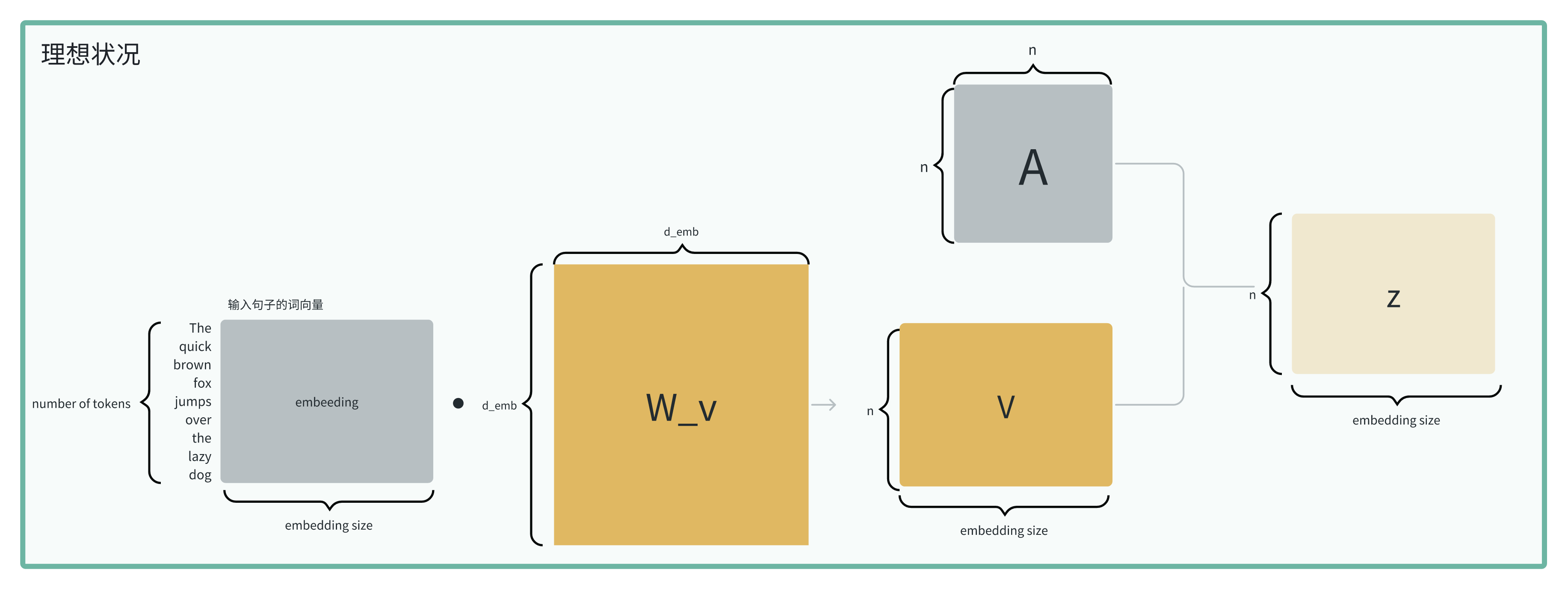
但实际上因为这个[d_emb, d_emb]的矩阵太大了,所以会拆成两个矩阵,一个up_project层,一个down_project层,中间的小维度就是d_v。而通常把第一个up_project层称为w_value。
d_v可以和dq, dk不同,因为它在作用时,是和n*n的矩阵进行相乘,和q,k的维度无关。
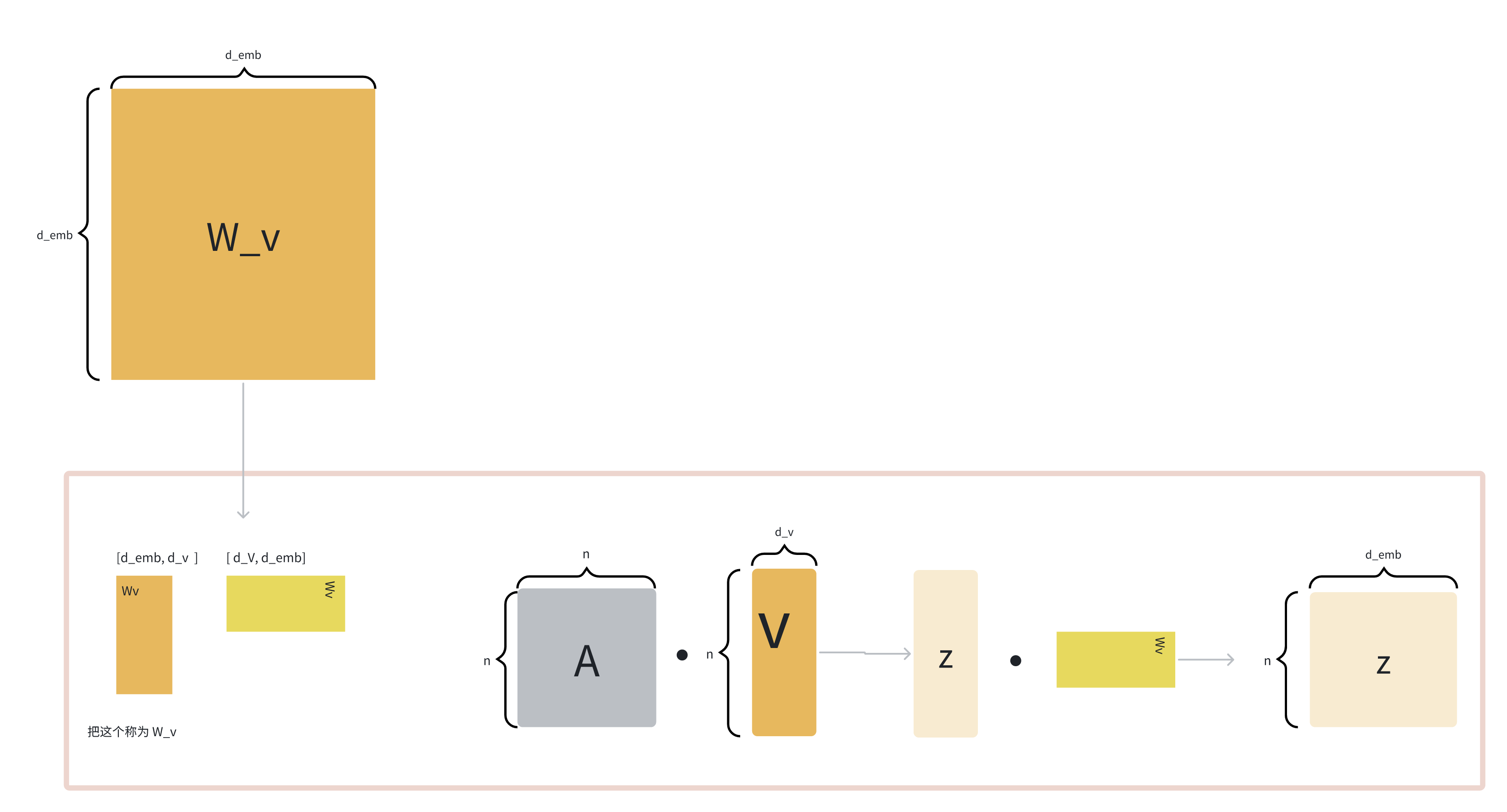
所以
参考文档
https://mp.weixin.qq.com/s/5TPYtEElfiSH8cHdu4uN7A
3b1b对self-attention的理解